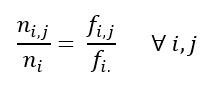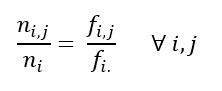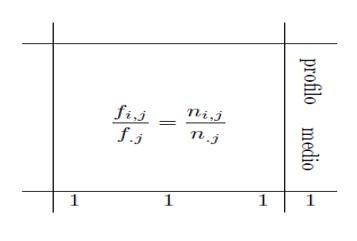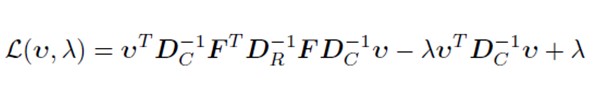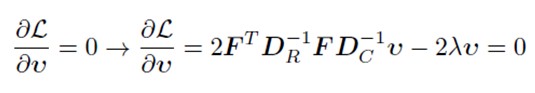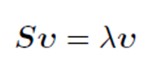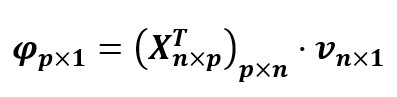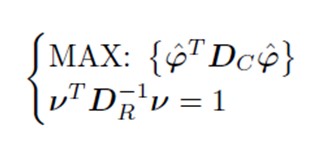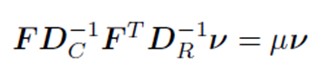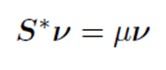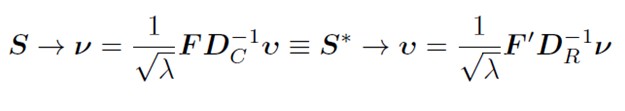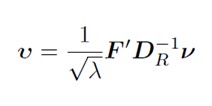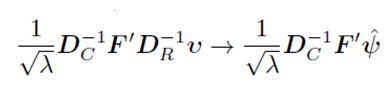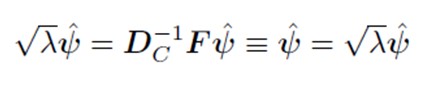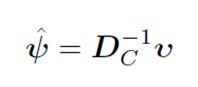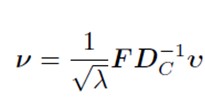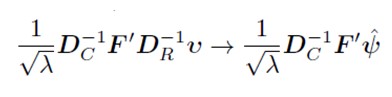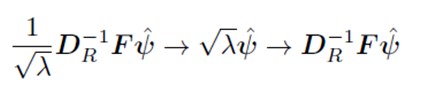Verificarea unei posibile relații între distribuția animalelor și diferitele regiuni italiene. Datele se referă la anul 2011, colectate de către băncile disponibile pe site-ul Istat.
Ipoteză: diferitele regiuni, în funcție de caracteristicile teritoriale și de nevoile populației, aleg să crească anumite capete de bovine mai degrabă decât altele.
Setul de date:

Importăm setul de date:
În câmpul "Row names" (Nume rânduri), selectați formularea: "use first column" (utilizați prima coloană) pentru a avea etichetele atât ale indivizilor, cât și ale variabilelor pe grafice. În câmpul zecimale, selectăm " comma " (virgulă).
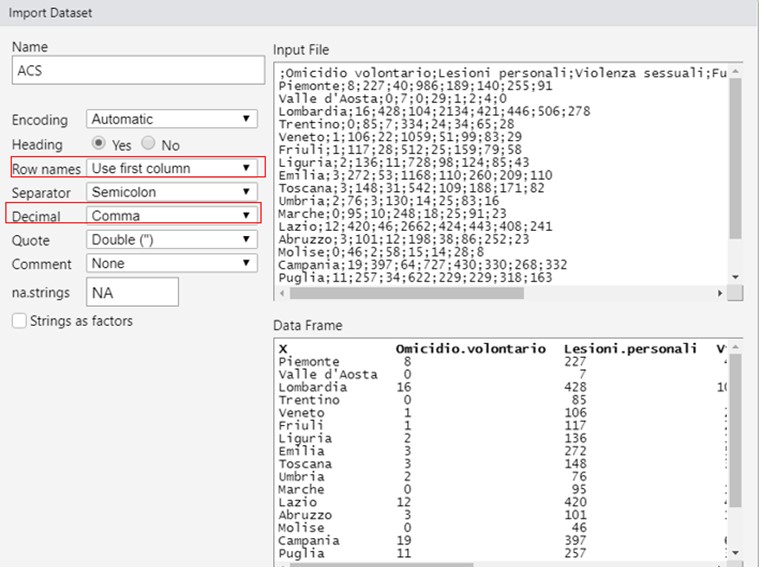
With the command:
X<-as.matrix(nome_del_dataset)
Atribuim lui X, ca obiect, setul de date utilizat în analiză.
Înainte de a putea efectua AC este necesar să se stabilească gradul de interdependență dintre cele două personaje luate în considerare, aceasta deoarece în cazul în care acestea sunt independente s-ar putea să nu aibă sens să se continue AC. Pentru a verifica acest lucru, efectuăm testul chi-pătrat.
chiquadro<-chisq.test(X)
Comanda este următoarea:

Se poate observa că valoarea p este mai mică decât nivelul de semnificație cel mai frecvent utilizat, și anume 0,05. Prin urmare, putem respinge ipoteza nulă de independență statistică între cele două variabile și putem continua analiza.
Acum dorim să creăm o matrice de frecvențe relative F.
Calculăm numărul de eșantioane, cu comanda:
n<-sum(X)
și apoi împărțind matricea de pornire (deci toate frecvențele comune) la numărul de eșantioane se obține matricea F. Comandă:
F<-X/n
Următorul pas este obținerea tabelelor de profiluri de rânduri și coloane. Pentru a face acest lucru, în primul rând, este necesar să se calculeze marginalele rândului și ale coloanei. Respectiv, comenzile sunt:
sumrow<-apply(F,1,sum)
sumcol<-apply(F,2,sum)
Apoi calculăm matricea diagonală a frecvențelor marginale de rând și inversa acesteia cu ajutorul comenzilor:
Dr<-diag(sumrow)
Dr_inv<-solve(Dr)
Acum putem calcula profilurile rândurilor. În termeni matriciali, înmulțim în prealabil inversa matricei diagonale a rândului marginal cu matricea frecvențelor relative. Comanda care trebuie folosită este:
Pr<-Dr_inv%*%F
Același lucru pentru profilurile coloanelor, ținând cont de faptul că, în acest caz, inversa matricei coloanelor trebuie să fie post-multiplicată la matricea frecvențelor relative.
Dc<-diag(sumcol)
Dc_inv<-solve(Dc)
Pc<-F%*%Dc_inv
Acum putem calcula distanțele dintre puncte. După cum am menționat deja, există două tipuri de distanțe: Euclidiană și Chi-pătrat.
Profilele rândurilor de distanțe euclidiene sunt:
d_euc_r<-dist(rbind(Pr[1,],Pr[2,]))
Profilele coloanelor de distanțe euclidiene sunt:
d_euc_c<-dist(rbind(Pr[,1],Pr[,2]))
Profilele rândurilor de distanțe chi-pătrat sunt:
d_r<-pr[1,]-pr[2,]
d<-d_r^2/sumcol
d_chi_r<-sqrt(sum(d))
Profilele coloanelor de distanțe chi-pătrat sunt:
dc<-Pr[,1]-Pr[,2]
dc<-dc^2/sumrow
d_chi_c<-sqrt(sum(dc))
Ecuația caracteristică a matricei profilului de rânduri:
S<-t(Pr)%*%Pc
Deoarece matricea S nu este simetrică, este necesar să o diagonalizăm pentru a obține S_tilde:
A<-t(F)%*%Dr_inv%*%F #simmetria
Dc_12<-diag(sumcol^(-1/2))
S_tilde<-Dc_12%*%A%*%Dc_12
Acum trebuie să maximizăm inerția explicată prin descompunerea matricei în valori proprii și vectori proprii:
AC<-eigen(S_tilde)
lambda<-as.matrix(AC$values)
lambda<-lambda[-1,]
w<-AC$vectors
u<-Dc^(1/2)%*%w
u<-u[,-1]
Ecuația caracteristică a matricei profilului de coloane:
S_star<-F%*%Dc_inv%*%t(F)%*%Dr_inv
Pentru a ne deplasa de la u la v, folosim formule de tranziție (deoarece cantitatea de inerție explicată este egală atât în spațiul rândurilor, cât și în cel al coloanelor).
sq_lambda<-diag((sqrt(lambda))^(-1))
v<-F%*%Dc_inv%*%u%*%sq_lambda
Calculăm factorii și coordonatele, mai întâi spațiul rândurilor și apoi al coloanelor:
fp_r<-Dc_inv%*%u
fp_c<-Dr_inv%*%v
PHI_coord<-Dc_inv%*%t(F)%*%fp_c
PSI_coord<-Dr_inv%*%F%*%fp_r
Se afișează graficul coordonatelor principale:
PRINCOORD<-rbind(PSI_coord,PHI_coord)
rows<-row.names(X);columns<-colnames(X)
plot(PRINCOORD[,1],PRINCOORD[,2],type="n",
main="Main Coordinates",xlab="Axis1",ylab="Axis2")+ text(PRINCOORD[1:20,1],PRINCOORD[1:20,2],labels=rows,col="springgreen4")
text(PRINCOORD[21:29,1],PRINCOORD[21:29,2],labels=columns,col="violetred")
abline(h=0,v=0,lty=2,lwd=1.5)
Rezultă:
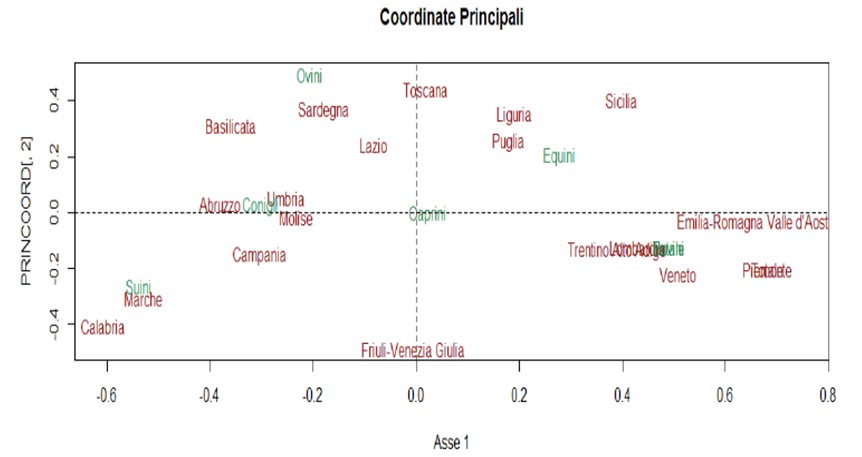
Dacă ne uităm la acest grafic, putem spune, de exemplu, că în regiuni precum Abruzzo, Molise, Umbria se cresc în principal iepuri.
Alegem componentele
inertia<-sum(diag(S))-1
sum(lambda)
in_exp<-lambda/inertia
in_exp_<-cumsum(in_exp)
Vizualizăm rezultatele obținute:

Prima dimensiune explică singură 58,57% din variabilitate, iar primele trei împreună explică 92,26% din variabilitatea globală a datelor.
Rezultatele obținute pot fi afișate grafic cu ajutorul graficului scree-plot a inerției explicate:
screeplot<-barplot(in_exp,main="Scree-plot inertia", xlab="Size", ylab="Lambda", col="lightblue")
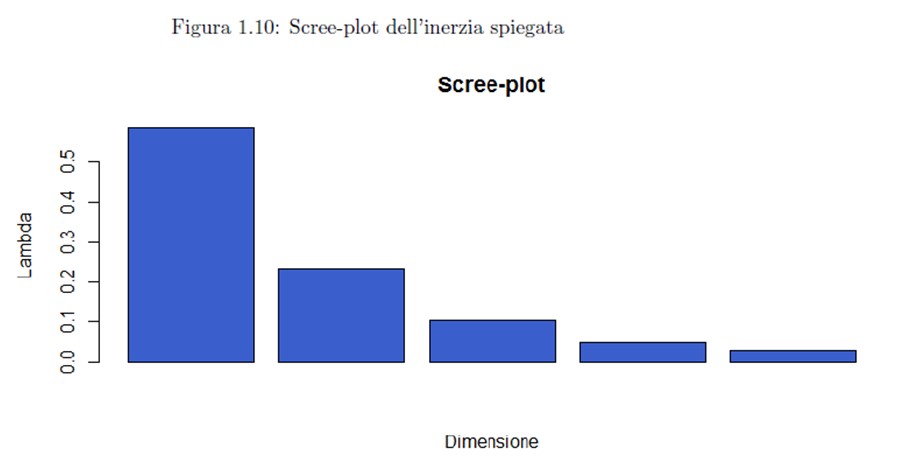
Pentru calitatea reprezentării:
- pentru a evalua cât de mult influențează sau participă un mod la axa factorială, se calculează contribuțiile absolute, CA, atât pentru rânduri, cât și pentru coloane:
ca_r<-Dr%*%fp_c^2
ca_c<-DC%*%fp_r^2
- Pentru a evalua calitatea reprezentării, calculăm contribuțiile relative, CR. Acestea oferă o măsură mai bună a reprezentării punctelor pe axe și este dată de cosinusul unghiului format de vectorul de proiecție al punctului și vectorul relativ i (sau j) în punctul i (sau j) din spațiul său original:
G<-matrix(sumcol,20,9,byrow=T)
di<-(Pr-G)^2%*%Dc_inv
d_ig<-apply(di,1,sum)
cos2r<-PSI_coord^2/d_ig
H<-matrix(sumrow,20,9)
dj<-Dr_inv%*%(Pc-H)^2
d_jh<-apply(dj,2,sum)
COS2C<-PHI_coord^2/d_jh
R oferă un pachet numit FactoMineR pentru analiza corespondențelor, care adaugă informații despre indivizi și variabile și vă permite să creați un grafic bidimensional comun al indivizilor și variabilelor.
Pe R pentru a putea utiliza acest pachet trebuie mai întâi să îl descărcați:

După ce l-ați instalat, trebuie să îl apelați cu comanda
library(FactoMineR)
Să trecem la crearea graficului bidimensional Persoane și variabile:
CA(X, ncp = 5, row.sup = NULL, col.sup = NULL, quanti.sup=NULL, quali.sup = NULL, graph = TRUE, axes = c(1,2), row.w = NULL)
Grafic, obținem:
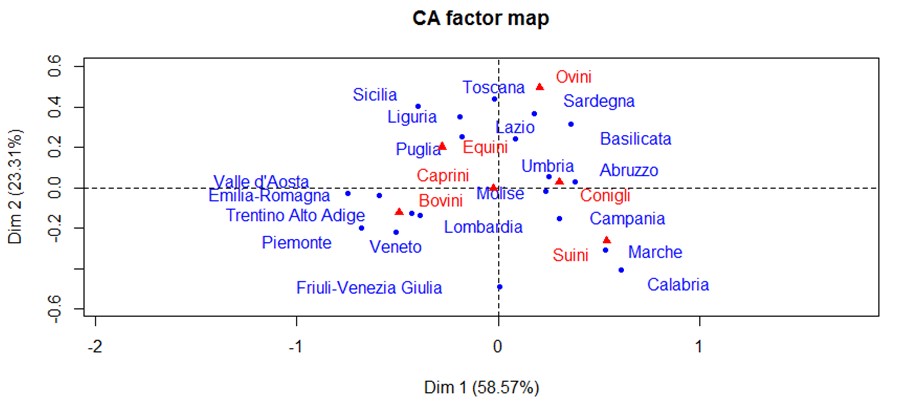
Interpretarea rezultatelor:
Putem spune că ipoteza inițială este confirmată. În special, regiunile cele mai dedicate creșterii ovinelor par a fi Toscana, Sardinia și Basilicata, iar acest lucru poate fi explicat prin faptul că aceste regiuni sunt zone de munte și de transhumanță. Caii sunt crescuți mai ales în Puglia, Liguria și Sicilia, deoarece aceste animale au fost întotdeauna folosite pentru muncă în mediul rural. Bovinele sunt prezente în Trentino Alto-Adige, Veneto, Piemont, Lombardia și Emilia-Romagna; de fapt, aceste regiuni au o tradiție de creștere mai dezvoltată pentru uz alimentar. Iepurii apar mai ales în Umbria, Abruzzo și Molise. În schimb, porcii par să fie crescuți mai mult în Marche, Campania și Molise; Aceste regiuni au, de asemenea, o tradiție de creștere mai dezvoltată pentru uz alimentar.
Caprele, pe de altă parte, sunt plasate la mijlocul axei, probabil pentru că nu există regiuni care să prefere creșterea lor.
 Redare audio
Redare audio