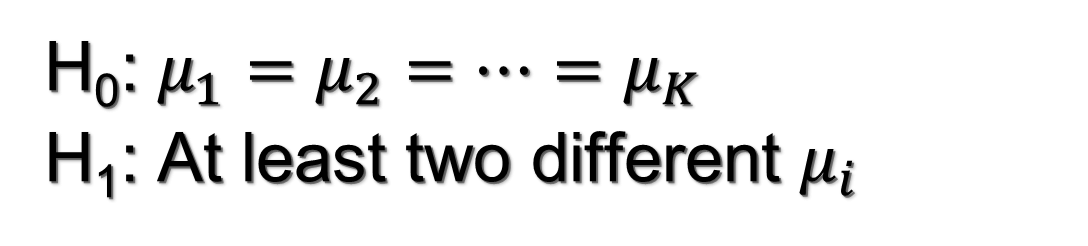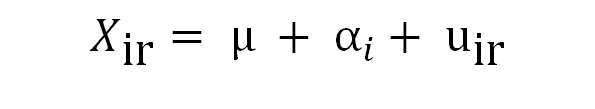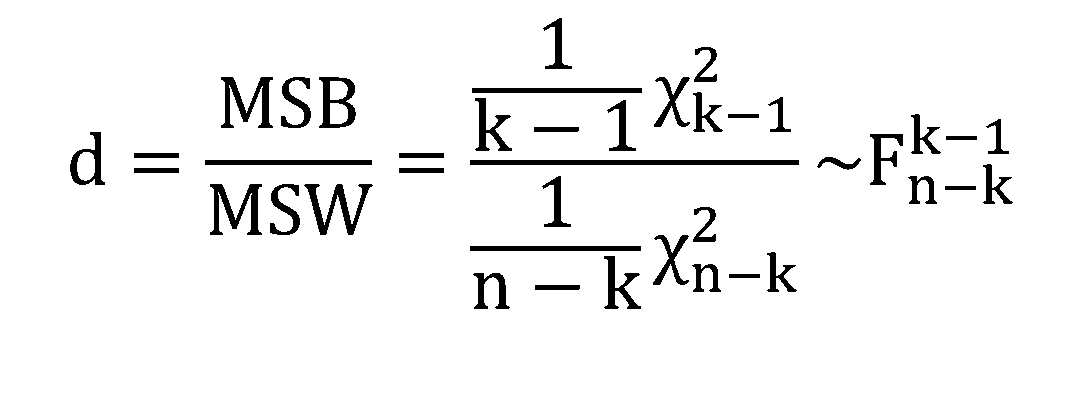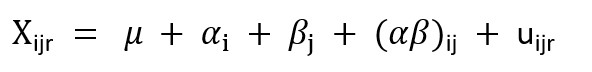DataScience Training
Keywords
Análisis multivariante, variabilidad inter e intra, comprobación de hipótesis, modelos lineales
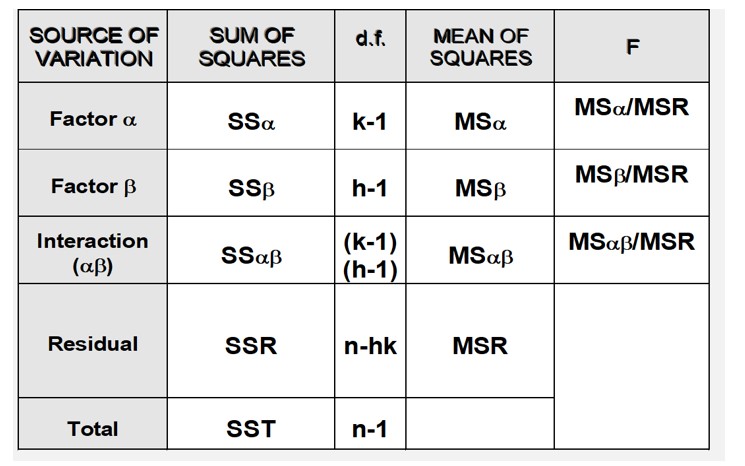
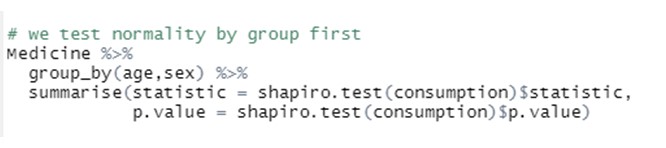
Objectives/goals:El objetivo de este módulo es presentar los conceptos básicos del análisis de la varianza (ANOVA) de uno y dos factores, que puede entenderse como un modelo lineal básico.
Al finalizar este módulo será capaz de:
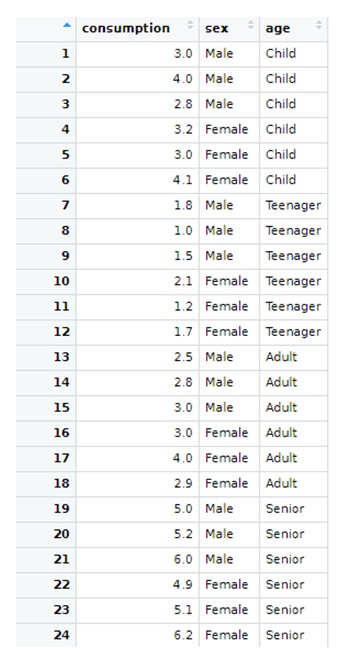
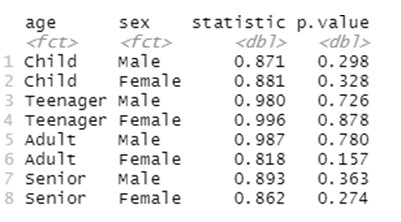
Cómo ANOVA puede ser útil para probar si existen diferencias entre el valor medio de una variable continua a través de diferentes niveles de una o varias variables categóricas.
Comprender e identificar las condiciones necesarias para aplicar estas técnicas.
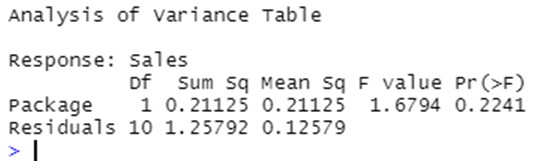
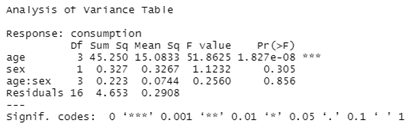
Realizar análisis de varianza unidireccionales y múltiples e interpretar los resultados obtenidos.
En este módulo se le presentarán los conceptos básicos del análisis de la varianza (ANOVA) de uno y dos factores, que puede entenderse como un modelo lineal básico.
En este curso aprenderá cómo ANOVA puede ser útil para probar, comprender e identificar las condiciones necesarias para aplicar estas técnicas y realizar análisis de varianza unidireccionales y múltiples e interpretar los resultados obtenidos.
NEWBOLD, P. et al. (2008): Statistics for Management and Economics, (6th edition) Ed. Prentice Hall. Chapter 17, pp. 635-661
Related training material
 Reproducir el audio
Reproducir el audio