obiectivul acestui modul este de a prezenta conceptele de bază ale analizei varianÈ›ei cu un È™i doi factori (ANOVA), care pot fi înÈ›elese ca un model liniar de bază.
La sfârÈ™itul acestui modul vei putea:
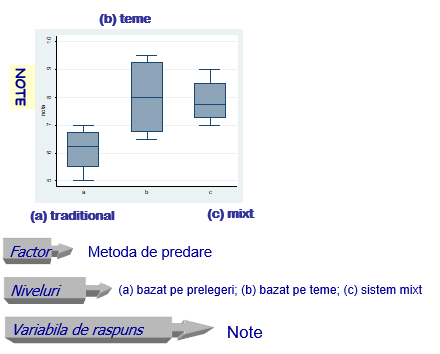
Cum poate fi utilă ANOVA pentru a testa dacă există diferenÈ›e între valoarea medie a unei variabile continue la diferite niveluri ale uneia sau mai multor variabile categoriale

ÎnÈ›elege È™i identifica condiÈ›iile necesare pentru aplicarea acestor tehnici

Efectua o analiză a varianței unidirecțională și multiplă și interpreta rezultatele obținute

Definim o variabil? de r?spuns, o variabil? continu? de interes

ÃŽn plus, avem informa?ii despre diferitele categorii ale unei variabile calitative. Aceast? variabil? categorial? se nume?te factor, iar fiecare categorie posibil? se nume?te nivel

Valoarea medie (neobservat?) a variabilei noastre de r?spuns la nivelul ? se noteaz? ?_?

Tehnicile GLM prezentate aici sub forma ANOVA permit răspunsul la întrebări potenÈ›ial interesante. Cateva exemple:

Lucrătorii bărbați și femei dintr-o regiune realizează același salariu mediu anual?

Studenții unui curs care urmează metode de predare diferite obțin aceeași notă medie?

Consumul mediu săptămânal al anumitor medicamente este diferit în funcÈ›ie de grupele de vârstă È™i/sau de sex?

ANOVA cu un singur factor este potrivită pentru întrebările 1 È™i 2, în timp ce întrebarea 3 necesită ANOVA cu doi factori
 

Să presupunem că avem un eÈ™antion de studenÈ›i, toÈ›i care urmează acelaÈ™i curs, repartizaÈ›i în clasele a, b È™i c

Elevii clasei (a) urmează o metodă tradiÈ›ională de predare bazată pe prelegeri. Elevii de la (b) urmează un sistem bazat pe teme, în timp ce studenÈ›ii de la (c) urmează un sistem mixt

Avem date eÈ™antion despre distribuÈ›ia notelor lor (scala de la 0 la 10) aÈ™a cum este reprezentată în boxplot

Dorim să testăm dacă există diferenÈ›e semnificative statistic privind notele lor medii, în funcÈ›ie de metoda de predare aplicată
 

Scop. Pentru a testa efectul unei variabile independente (FACTOR) clasificată în mai multe categorii k (NIVELURI) asupra unei variabile dependente numerice (VARIABILÄ‚ DE RÄ‚SPUNS)

Se bazează pe descompunerea variabilității totale a eșantionului

Putem aborda această problemă ca un test de ipoteză statistică a unei ipoteze nule (H0; implicită) față de alternativă (H1; o viziune alternativă asupra lumii)

Testul este formulat în funcÈ›ie de media variabilei răspuns la nivelurile factorului nostru
 

Ipotezele necesare pentru efectuarea testului ANOVA sunt
 PopulaÈ›ii normale: distribuÈ›ia variabilei răspuns la fiecare nivel ar trebui să fie normală
 Egalitatea varianÈ›elor: variaÈ›iile variabilei răspuns între niveluri trebuie să fie aceleaÈ™i
 EÈ™antioane independente: datele eÈ™antionului de la fiecare nivel al factorului nu sunt corelate cu celelalte date ale eÈ™antionului (colectate de la celelalte niveluri)
 

Se ia eÈ™antionul de date pe X È™i descompunem variabilitatea acesteia (dispersia în jurul mediei eÈ™antionului) în două părÈ›i:

În cadrul grupului (SSW) È›ine cont de variabilitatea internă
Variabilitatea între (SSB) reprezintă diferenÈ›ele dintre media eÈ™antionului fiecărui grup È™i media mare

Variabilitatea totală (SST) este doar suma SSW+SSB

Dacă SSB este mult mai mare decât SSW, se sugerează că există diferenÈ›e semnificative între mediile grupului. Deci, vor exista diferenÈ›e semnificative în ceea ce priveÈ™te mediile între nivelurile factorului

Descompunerea variabilității

Pentru a compara ponderea relativă a SSB È™i SSW asupra variabilității totale, le-am scalat împărÈ›ind la numărul de grade de libertate, producând valorile MSB È™i respectiv MSW

Dacă ipotezele necesare sunt valabile, statistica (d) calculată ca MSB∕MSW se distribuie ca un model F

x_"ijr"  este valoarea variabilei noastre de răspuns pentru individul r la categoria (nivelul) i al factorului α È™i nivelul j al factorului  β
Presupunem că aceste valori se îndepărtează de marea medie ("μ"), ca suma a patru efecte:

O schimbare ("α" _i ) care surprinde influenÈ›a medie a apartenenÈ›ei la nivelul i al factorului α
O a doua schimbare (β_j) care surprinde influenÈ›a medie a apartenenÈ›ei la nivelul j al factorului β 
Un termen de interacÈ›iune între aceÈ™ti doi factori (αβ)_"ij"   
O eroare  "u" _"ir" , care explică variaÈ›ii aleatorii, necontrolate. Se presupune că acest rezidual se distribuie normal cu medie zero

Testul ANOVA este acum extins pentru a lua în considerare un al doilea factor plus o posibilă interacÈ›iune

Acum, comparațiile dintre diferitele părți ale variabilității sunt mai complexe

Fiecare sursă de variaÈ›ie este comparată (scalată în mod convenabil după numărul de grade de libertate) cu varianÈ›a reziduală

IntuiÈ›ia este aceeaÈ™i ca È™i în cazul ANOVA cu un singur factor, dar există trei teste diferite

O instituÈ›ie sanitară doreÈ™te să analizeze potenÈ›iala influență a vârstei È™i sexului asupra utilizării unui medicament. În acest scop este realizat un sondaj pe un eÈ™antion, iar utilizatorii au fost grupaÈ›i în funcÈ›ie de vârstă în patru categorii (copii, adolescenÈ›i, adulÈ›i, seniori) È™i sex.

Un sondaj pe un eÈ™antion este realizat în acest scop È™i utilizatorii au fost grupaÈ›i pe vârstă în patru categorii (copii, adolescenÈ›i, adulÈ›i, seniori) È™i sex. A fost extras un eÈ™antion de 24 de persoane, selectând în mod independent 3 persoane în funcÈ›ie de sex È™i grup de vârstă.

Variabila de răspuns este consumul lunar al acestui medicament (în €),

Testăm mai întâi dacă ipotezele necesare sunt valabile, rulând testul de normalitate È™i varianÈ›e egale. Teste de normalitate (pentru toate grupele de vârstă È™i cele două sexe):

Ambele teste sunt trecute, astfel încât ANOVA cu doi factori poate fi efectuată